The Lifelong Learner

Trong bài viết này, mình muốn giới thiệu cho các bạn về Value At Risk hay gọi tắt là VaR. Một trong những công cụ đo lường rủi ro rất phổ biến, được sử dụng rộng rãi nhất khi tính rủi ro thị trường (market risk), nhưng cũng không kém phần quan trọng trong cách tính tài sản rủi ro tín dụng (risk weighted asset credit risk) theo mô hình Basel.

Bài viết này sẽ tập trung làm rõ những điểm sau đây:

1. Ý tưởng nôm na của VaR
2. Tản mạn về thống kê
3. Những cách tính VaR phổ biến

Mình hy vọng là bài viết này có thể giúp mọi người hiểu rõ về công cụ này, vì nó sẽ còn theo đuổi chúng ta dài dài trên hành trình tìm hiểu về quản trị rủi ro trong và ngoài môi trường ngân hàng.

Ý tưởng về VaR

Mình sẽ nhắc lại một chút về định nghĩa của rủi ro mà mình đã viết trong bài viết trước đây.

Khi chúng ta hướng tới một mục tiêu nào đó thì tất cả những “bất trắc” mà chúng ta có thể gặp phải, làm cho chúng ta “có thể” bị “chệch” khỏi mục tiêu đó được gọi là rủi ro.

Như vậy, bản thân định nghĩa của rủi ro đã chứa đựng hai yếu tố rất quan trọng là xác xuất mà những sự việc “bất trắc” có thể diễn ra và ảnh hướng (độ chệch) của nó đến với mục tiêu của mình

Công cụ VaR tập trung vào việc dựa trên những dữ liệu sẵn có để “ước lượng” sự ảnh hưởng của những trường hợp xấu nhất mà chúng ta có thể gặp phải.

Mình sẽ dùng ví dụ thường ngày sau đây để đơn giản hóa khái niệm về VaR…

Mỗi sáng bạn đi làm, mục tiêu của bạn là cố gắng để đến chỗ làm đúng giờ nhất có thể. Tất nhiên là đến sớm được thì sẽ rất tốt, bạn có thời gian để giải quyết rất nhiều công việc trước khi giờ làm bắt đầu. Còn trường hợp xấu là bạn đi muộn, mỗi lần đi muộn thì chắc chắc là hình ảnh của bạn đối với sếp sẽ xấu đi, nhất là nếu bị lỡ một cuộc họp quan trọng gây thiệt hại lớn trong công việc thì tình hình lại càng tồi tệ.

Tuy nhiên, dù rất cố gắng thì bạn cũng không thể đảm bảo được là trong 100 ngày, bạn luôn luôn đạt được mục tiêu ở trên. Có khoảng 50 ngày thì hành trình đến chỗ làm của bạn đúng như bạn tính toán. Có khoảng 25 ngày thì bạn cảm thấy tinh thần khỏe mạnh, ngủ dậy sớm hơn nên bạn đến sớm hơn thường ngày. Còn trong 25 ngày còn lại, vì nhiều lí do khác nhau như ngủ dậy trễ, bận một số công việc ở nhà, chăm sóc người ốm hay tắc đường mà bạn đều đến chỗ làm muộn.

Hơn nữa, trong số 25 ngày đi muộn này, lại có một ngày đặt biệt hơn…

Như thường ngày, bạn dậy sớm trước 1 tiếng, ăn mặc chỉnh tề, check giờ phương tiện công cộng. Theo đúng lộ trình mà ứng dụng tàu điện đưa ra, bạn chỉ cần bước lên tàu đi khoảng 5 bến là đến nơi bạn làm việc. Tuy nhiên vừa mới đi được khoảng 3 bến thì người lái tàu thông báo với bạn rằng đường ray phía trước bỗng nhiên gặp sự cố do có một hành khách gặp tai nạn. Các cơ quan chức năng như công an và bệnh viện phải vào cuộc. Toàn bộ hệ thống tàu điện bị “tê liệt” trong khoảng 1 tiếng đồng hồ. Còn bạn? Bạn bị kẹt trong khoang tàu, nội bất xuất, ngoại bất nhập. Chỉ sau khi mọi chuyện được giải quyết thì chuyến tàu mới được tiếp tục. Kết quả là bạn đi làm muộn 1 tiếng.

Trong ví dụ ở trên, khoảng thời gian “muộn 1 tiếng” có thể coi như một dạng VaR. Nghĩa là khi một trường hợp rất xấu diễn ra, thì độ “chệch” so với mục tiêu đi làm đúng giờ của bạn là 1 tiếng đồng hồ. Tuy nhiên, những tình huống cực đoan như vậy thường sẽ rất hi hữu, nó chỉ xảy ra vào 1 trong 100 ngày bạn đi làm, tức là xác xuất của nó là 1%.

Mục tiêu của công cụ VaR là dựa trên những dữ liệu quan sát được, để “dự đoán” độ “chệch” cực đoan với xác xuất xảy ra là 1% như ở ví dụ trên.

Tản mạn về thống kê

Bây giờ, chúng ta hãy dùng ví dụ ở trên để cụ thể hóa về một số kiến thức thống kê cơ bản. Nếu chúng ta phân chia “quan sát” về thời gian đi làm trong 100 ngày thành ba nhóm là “đi sớm”, “đúng giờ” và “đi muộn” thì chúng ta sẽ có sự phân phối (distribution) như sau.

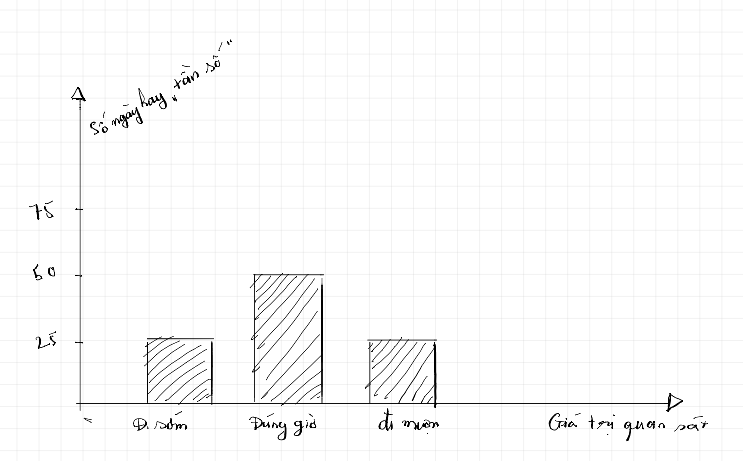
Nhưng nếu chia giá trị quan sát vào 3 nhóm như vậy thì độ chi tiết sẽ không cao và chúng ta không thể nhìn ra được những giá trị cực đoan (như khi đi làm muộn tận 1 tiếng như sự kiện ở trên). Vì vậy, thay vì dựa vào 3 nhóm giá trị ở trên, chúng ta có thể chia nhỏ giá trị quan sát của mình thành thời gian đi làm sớm hoặc muộn theo phút.

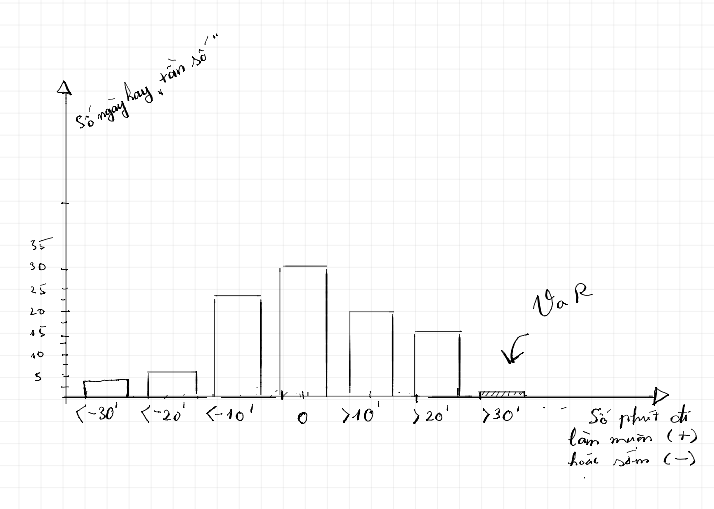
Trong biểu đồ 2, chúng ta đã “đếm” số ngày đi làm sớm, đúng giờ hoặc làm muộn dựa trên số phút đi làm muộn hoặc sớm (với số phút đi muộn là giá trị dương và số phút đi sớm là giá trị âm). Theo đó, chúng ta có 4 ngày đi làm sớm hơn 30 phút , 6 ngày làm sớm hơn 20 phút, 24 ngày làm sớm hơn 10 phút, 30 ngày trong khoảng cộng trừ 10 phút, v…v…. Hơn nữa, chúng ta có thể thấy rằng, trong 100 ngày này, chỉ có đúng 1 ngày chúng ta đi làm muộn hơn 30 phút, đó chính là ngày mà chúng ta bị mắc kẹt ở trên tàu. Như vậy, giá trị VaR với xác xuất 1 phần trăm ở đây là “hơn 30 phút” (muộn 1 tiếng cũng được xếp vào hơn 30 phút).

Nói một cách khác, theo mô hình VaR ở trên thì xác xuất mà bạn đi làm muộn tối đa là 30 phút rơi vào khoảng 99%. Chỉ trong 1% hi hữu, trong một trường hợp rất xấu, thì bạn mới đi làm muộn trên 30 phút.

Trong thống kê, quá trình sắp xếp giá trị của những quan sát theo thứ tự từ lớn đến nhỏ và đếm tần số của những giá trị đó còn gọi là tính phân vị (quantile). VaR sẽ thường được tính dựa trên một phân vị có xác xuất cao (như 99%), vì khả năng mà một giá trị cao hơn phân vị đó được hiện thực hóa là rất thấp (100%-99% = 1%).

Những cách tính VaR phổ biến

Như ở trong ví dụ ở trên, để tính được VaR thì chúng ta cần dựa trên dữ liệu có sẵn để xác định được phân phối xác suất (statistical distribution) của những sự kiện mà mình quan tâm. Tuy nhiên, để xác định phân phối xác suất này thì chúng ta gặp phải 2 vấn đề:

1. Chúng ta thường không thể quan sát được tất cả các sự kiện (polulation). Ở trong ví dụ trên, chúng ta đã ước lượng phân phối xác suất dựa trên quan sát các sự kiện trong một “mẫu thử” có giới hạn là 100 ngày. Tuy nhiên, điều chúng ta thực sự quan tâm là phân phối xác suất thực sự của những sự kiện, không bị phụ thuộc và giới hạn vào tính chất của mẫu thử.
2. Điều chúng ta quan tâm là giá trị VaR trong tương lai. Vì vậy, chúng ta không chỉ đơn giản là sử dụng dữ liệu ở quá khứ, mà cần phải áp dụng một số phương pháp và giả thuyết để dự đoán phân phối xác suất ở tương lai.

Theo các tài liệu nghiên cứu, có 3 phương pháp tính VaR thường được áp dụng nhất là mô phỏng quá khứ (historical simulation), mô phỏng tham số (parametric simulation), và mô phỏng Monte-Carlo (monte carlo simulation).

Mình sẽ không đi quá sâu về mặt toán học và thống kê của những phương pháp trên nhưng sẽ tóm tắt lại một số đại ý về chúng.

Mô phỏng quá khứ dựa trên giả thuyết là phân phối xác suất trong quá khứ sẽ không thay đổi và được lặp lại. Vì thế, giá trị VaR ở quá khứ là biểu hiện của giá trị VaR trong tương lai. Cách tính VaR trong ví dụ ở trên của mình chính là dựa trên phương pháp này.

Mô phỏng tham số thì dựa trên giả thuyết là phân phối xác suất thực sự thường sẽ tương tự như một số phân phối xác suất trên lý thuyết (ví dụ như phân phối xác suất chuẩn ~ normal distribution, hay phân phối xác suất student-t ~ student-t distribution). Vì vậy, thay vì trực tiếp ước lượng phân phối xác suất thì phương pháp này sẽ ước lượng tham số của những xác suất này để từ đó xác định được xác suất phân phối.

Cuối cùng là phương pháp Monte-Carlo, lấy cảm hứng từ sòng bạc Monte Carlo ở Monaco. Phương pháp này sử dụng một khái niệm trong thống kê được gọi là quá trình ngẫu nhiên (stochastic) để mô phỏng sự hoạt động cũng như kết quả của sự kiện. Sau đó, phân phối xác suất sẽ được tính dựa trên những sự kiện được mô phỏng đó.